学术报告:量子计算的布局综合
报告简介
2020年7月19日由UCLA博士生谭伯琛给我们带来题为量子计算的布局综合的报告。谭同学主要介绍他们构造的一类量子线路基准测试程序 QUEKO Benchmarks(QUantum Mapping Examples with Known Optimal,https://vast.cs.ucla.edu/software/queko-benchmarks),它们具有已知的最优深度[1]。可以使用QUEKO评估如图1量子计算流程中的Layout Synthesis(布局综合)阶段工具的最优性。
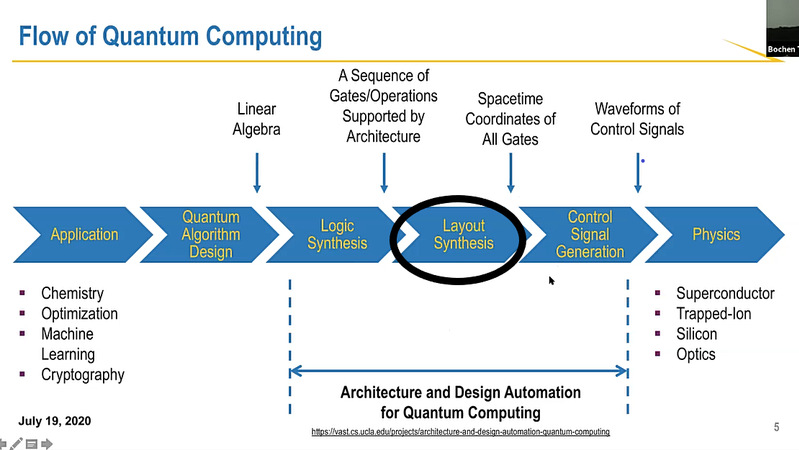
图1 量子计算流程
研究动机与贡献
目前评估不同布局综合工具优化技术的主流方法是,用它们优化同样的benchmarks然后比较它们产生的结果。然而,由于布局问题是NP难的,目前尚不清楚这些工具给出的结果距离最优解还有多远。为此,谭等人构造QUEKO benchmarks,这一类量子线路针对给定的量子计算设备结构有已知的最优解。然后,他们用QUEKO评估了Circ、t|ket〉、Qiskit和Zulehner等人2018年提出的量子比特映射算法这四种工具。他们发现即使对于可行深度的量子线路,这些工具得到的结果距最优解也有很大差距:在较小设备上平均为1.5-12倍,在较大设备上平均为5-45倍。
QUEKO Benchmark的构造方法
第一步:输入量子设备的量子比特连接图(如图2(a))、目标深度(如图2(b)的目标深度为3)和门密度参数。这些都是为了模仿真实的物理线路。
第二步:以Toffoli线路和给定量子比特连接图为基础,生长一系列T门,每个门取决于前一个,形成以指定目标深度为长度的依赖链(如图2(b))。这一步主要受谭伯琛的导师丛京生教授2003年发表的有关经典布局工作[2]的启发。
第三步:在依赖链的每一层,根据指定的门密度添加更多的门(如图2(c))。
第四步:产生从物理量子比特到逻辑量子比特的随机映射,即将它们的关系打乱(如图2(d)),从而得到不满足物理约束的量子线路(如图2(e))。
第五步:输出打乱后量子线路对应的 OpenQASM 文件(如图2(f)),形成benchmark。

图2 构造QUEKO线路
特色与效果
QUEKO提出了一种根据量子设备结构逆向构造benchmark的方法,所构造的量子线路具有已知最优解,然后再“加料打乱”。因为人们对于最优解具有很深的执念,所以QUEKO相当于给了参考答案,然后再去出题考编译器(布局综合工具)。
QUEKO Benchmark提供的量子线路最优解中是不会含有SWAP门的,并且量子线路具有<目标深度>=<最长依赖链的长度>的特点,这两点都是由其量子线路的构造方式决定的。
针对构造的QUEKO Benchmarks,谭等人用t|ket>等四种编译/布局工具进行了实验评测。t|ket>利用了Graph Placement的选项能够得到一个相对于其他算法更优秀的结果,这也一定程度上证明QUEKO的线路特点是很明确的。在四种工具上的实验也表明现有布局优化工具产生的结果距离最优解还有很大提升空间。
思考与启发
QUEKO Benchmark的构造方法潜在为寻找更好的布局策略提供了一种思路和实例素材。以评估量子优越性的quantum volume算法为例,该类算法含有大量CNOT门,但是我们并不知道它针对指定量子比特连接结构的最优解是多少,只能通过在不同的布局优化工具上跑benchmark进行比较来得出相对最好的解。而按照QUEKO的构造思路可以尝试构造出绝对最优解,让我们知道离终点线还有多远。
另一个值得深思的问题是,QUEKO针对量子设备结构给出的最优解真的就是这种量子设备的最优线路吗?由于QUEKO目前不考虑对易性和噪声,因此目前得出的“最优解”并不能是实际量子设备上的最优解。在考量对易性和噪声后,有可能会找到更好的结果(有了对易性可以交换门的位置,然后可以把串扰较小的门操作放在一起)。但是,正如实验表征的那样,现有的量子线路布局综合工具到参考答案的距离还有很远,更何谈超出这种最优解!
最后,在NISQ时代,含噪量子计算是我们必须面对的问题。未来QUEKO有可能会加入噪声模型,但是愿望是好的,在现实情况下怎么对噪声建模以及如何将噪声引入到工具中都会面对很多挑战。
参考文献
[1] Chin-Chih Chang, Jason Cong, Min Xie. Optimality and Scalability Study of Existing Placement Algorithms. ASP-DAC’03, pp:621-627, 2003. https://doi.org/10.1145/1119772.1119914
[2] Bochen Tan, Jason Cong. Optimality Study of Existing Quantum Computing Layout Synthesis Tools. IEEE Transactions on Computers. July 14, 2020. https://doi.org/10.1109/TC.2020.3009140
(本文编者:孟昱昊、张昱)

